
안녕하세요, 여러분! “인생꿀팁” 블로그에 오신 것을 환영합니다. 오늘은 전기 회로 이론에서 자주 사용되는 라플라스 변환 표에 대해 알아보려고 해요. 오늘은 전기 회로 이론에서 자주 등장하는 라플라스 변환 표에 대해 알아보려고 합니다.이 글을 통해 라플라스 변환이 무엇인지, 그리고 실생활에서 어떻게 활용될 수 있는지 쉽게 이해하실 수 있을 거예요.
라플라스 변환이란?
라플라스 변환은 시간 영역의 함수를 주파수 영역의 함수로 변환하는 수학적 기법이에요. 전기 회로 문제를 해결할 때 라플라스 변환을 활용하면 미분 방정식을 대수 방정식으로 바꿀 수 있어서 문제 해결이 쉬워집니다.
공대 수학의 꽃, 라플라스 변환표자주 사용되는 라플라스 변환 표
라플라스 변환 표에는 다양한 함수에 대한 라플라스 변환 공식이 정리되어 있어요. 이 표를 통해 복잡한 계산을 빠르고 정확하게 할 수 있답니다. 아래 표는 전기 회로에서 자주 사용되는 함수들과 그 라플라스 변환 결과를 정리한 것이에요.
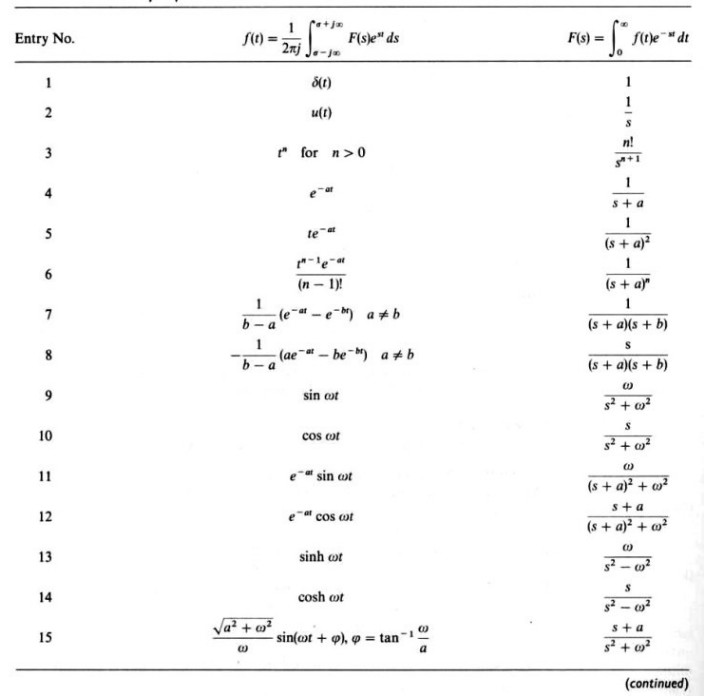
| 시간 함수 f(t) | 라플라스 변환 F(s) |
|---|---|
| 1 | 1/s |
| t | 1/s^2 |
| ( e^{-at} ) | 1/(s+a) |
| ( \sin(bt) ) | b/(s^2 + b^2) |
| ( \cos(bt) ) | s/(s^2 + b^2) |
이 표만 잘 활용해도 회로 분석이 훨씬 쉬워질 거예요.
라플라스 변환의 실생활 활용 사례
라플라스 변환을 활용하면 전기 회로 문제를 대수 방정식으로 변환할 수 있어서 문제 해결이 쉬워져요. 예를 들어 RC 회로의 과도 응답을 구할 때 라플라스 변환을 이용하면 간단히 구할 수 있죠.
전기 회로 해석
저는 최근에 친구와 함께 간단한 전기 회로를 분석해야 했는데요. 라플라스 변환 표를 활용하니 복잡한 미분 방정식을 쉽게 풀 수 있었어요. 정말 만족도 100%였는데요! 전압과 전류의 관계를 명확하게 이해할 수 있었답니다.
회로이론 _라플라스 변환표
제어 시스템 설계
또한, 제어 시스템 설계에서도 라플라스 변환은 필수적이에요. 예를 들어, 자동차의 크루즈 컨트롤 시스템을 설계할 때 라플라스 변환을 사용하면 시스템의 안정성을 쉽게 분석할 수 있어요. 덕분에 더 안전하고 효율적인 제어 시스템을 만들 수 있었답니다.
라플라스 변환 – 변환표라플라스 변환 표 활용 팁
라플라스 변환 표는 단순히 암기하는 것보다, 실제 문제에 적용해보는 것이 더 중요해요. 문제를 풀 때마다 표를 참고하면 자연스럽게 익숙해질 수 있답니다. 예를 들어, 주어진 전기 회로에서 저항(R), 인덕터(L), 커패시터(C)의 라플라스 변환을 각각 구해 전체 회로의 전달 함수를 구하는 연습을 해보세요.
아쉬운 점과 개선 방안
라플라스 변환은 강력하지만, 모든 문제를 해결해주지는 않아요. 예를 들어, 비선형 시스템에서는 적용이 어렵다는 단점이 있어요. 이런 경우에는 다른 수학적 도구나 방법론을 함께 사용해야 할 때도 있어요. 하지만 대부분의 선형 시스템에서는 매우 유용하니 꼭 익혀두세요.
유용한 링크
라플라스 변환에 대해 더 알고 싶다면 아래 링크를 참고해보세요. 유용한 정보들이 많답니다!
제가 직접 RC 회로 문제를 풀어보면서 느낀 점은, 라플라스 변환을 잘 활용하면 회로 문제 해결이 정말 쉬워진다는 거였어요. 처음에는 낯설었지만, 라플라스 변환 표를 활용하다 보니 문제 풀이 속도도 빨라지고 정확도도 높아졌죠.
여러분도 전기 회로 문제를 풀 때 라플라스 변환을 적극 활용해보세요. 처음엔 어려울 수 있지만, 익숙해지면 큰 도움이 될 거예요. 오늘 소개해드린 내용이 도움이 되었길 바랍니다. 행복한 하루 보내세요!





